Music & Audio Computing II Final Project

Modelling filters on a DJ controller

Zeyu Li

Motivation

The original goal of the project is to write a DJ mixing synthesizer. It would be able to synthesize the music mixes given a list of controlling sequences on onset, duration, tempo/pitch, volume, and EQ settings. To do that, I wanted to use existing STFT algorithms to process the audio files, and apply any time stretch, pitch bend, fader, filtering etc. as needed.

This synthesizer would be part of the automatic DJ system I am working on:

1. Record live control sequences on the DJ controller with the midi sequence parser for analysis
2. Feed new songs into a mixing algorithm that generates a mixing sequence for them
3. Synthesize the new mix from new songs and mixing sequence generated

Therefore, with step 1. and 3. completed, we can resynthesize the mixing audio from the control sequences recorded on the DJ controller. After this I can work on the the most important part of the project, the mixing algorithm that is built through either machine learning, expert rules, customization, or interaction with listener.

The Project Goal

After the project discussion, I realized that although there are existing time-stretch and pitch-bend algorithms ready to use, the filters on the DJ controller are not that straightforward to implement. Without knowing details of the filters involved, it would not be possible to resynthesize the same output result as from the controller.

Therefore I turned the focus of the project to determine the types of filters on a ©Pioneer DDJ-SX2 controller (low-cut, mid-cut and high-cut), and estimate the parameters of each of them. I completed this through 2 steps: first retrieve the filter response through comparing the filtered and unfiltered signal passing through the controller, then determine which type of filters is used, and obtain the filter coefficients through trial and error.

Retrieving Filter Response

I started by generating a chirp signal of 5 seconds with the frequency linearly increasing from 0 to 22050 Hz (see Chirp.m and Chirp.wav):

It looks like this on a spectrogram:

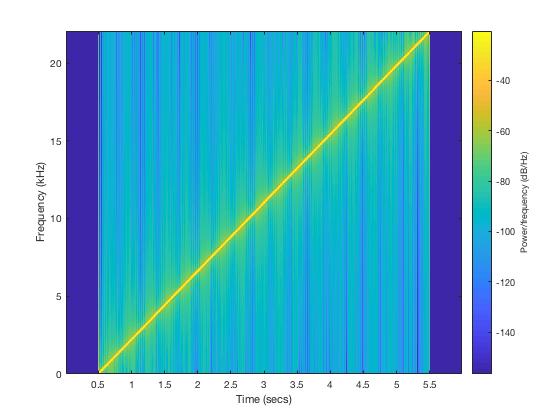
After sending the signal through the controller, I applied the STFT on the recorded result, and obtained the filter response on a log frequency-dB scale (see Analysis.m and LowCutLinear.wav):

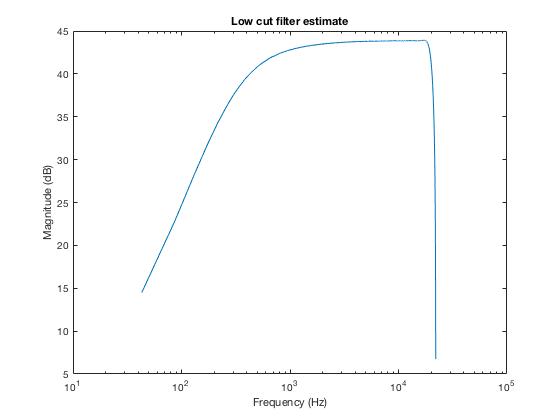
(It should be noted here that the high end frequencies are automatically cut off by the DJ controller)

I discovered that even though overall the magnitude frequency response looks smooth, the low end only extends to 30 Hz, and it can be observed that the precision is low below 200 Hz.

Other issues include that the dB scale is wrong, and where the low filter does not apply the overall frequency response is not flat, even though the energy of our input signal is spread evenly across all frequency bands.

To address the deficiencies, I regenerated another chirp signal on a log-frequency scale (see LogChirp.m and LogChirp.wav):

The signal looks like this on a spectrogram:

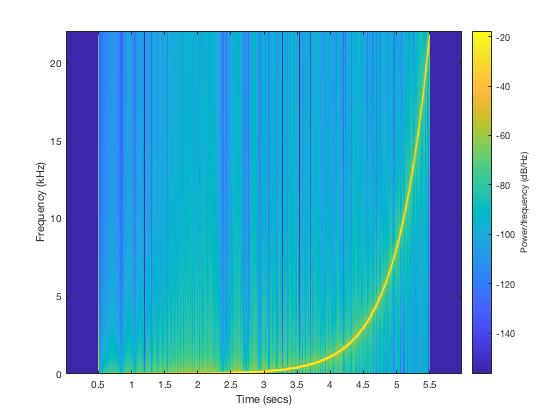
To ensure the signals are aligned when comparing the frequency responses, I also generated a click at the beginning, and aligned the recordings based on it. (see LogChirp.m and LogAnalyzer.m)

Then I recorded the signal filtered by the DJ controller, and calculated the frequency response of the filters, by dividing peak energy at each frequency band of the filtered signal by the unfiltered signal (passing through the controller with all filters set to neutral). After doing this for 14 notches on the low filter, I obtained a figure of the frequency response of each filter on different filter notches (see LogAnalysis.m, LogFlat.wav and LogLowCut*.wav):

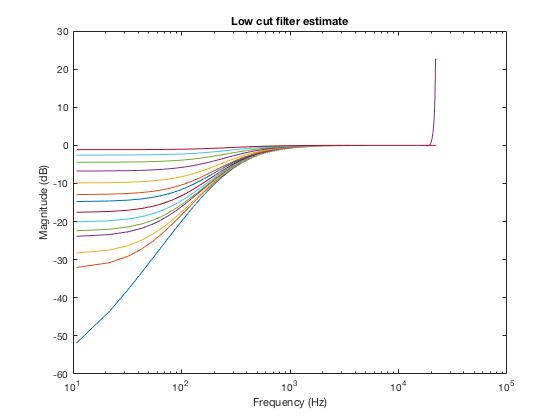
Applying the same methodology to the mid and high filters (see LogMidCut*.wav and LogHighCut*.wav):

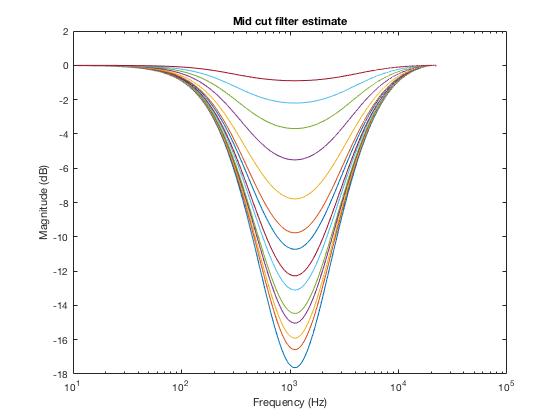
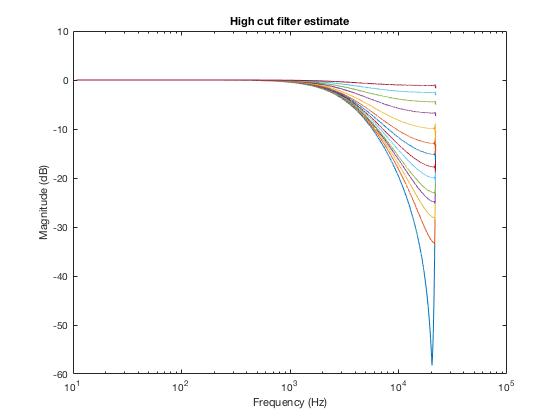
Retrieving filter coefficients

As the course instructor suggested, the low and high filters appear to be second-order shelving filters [1], and mid filter being the second-order peak filter, so I modelled the filters based on an implementation by Tackett [2, 3] (shelving.m and peaking.m).

To map the filter model coefficients back to the DJ controller, I recorded the MIDI notch values (0-64) of the filter knobs when I recorded the signal output, through the DJ MIDI Sequence Parser I built for the MUMT 306 final project in Fall 2017.

Through carefully tuning each coefficient, I obtained the filter response close to the output signal (see FilterModel.m):

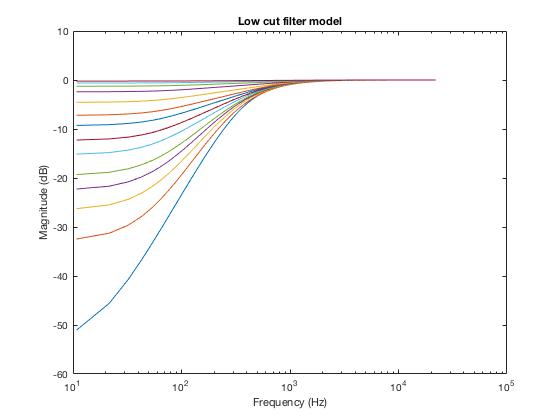
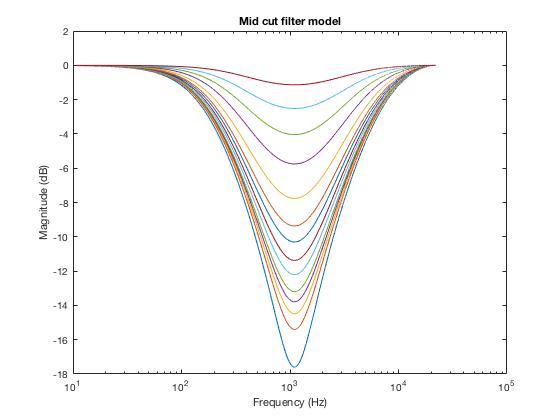
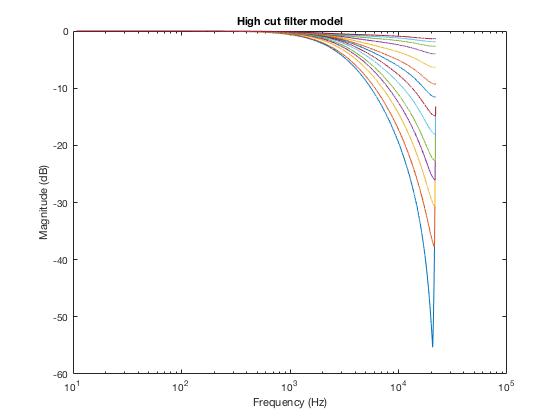
As can be seen, the modelled filter frequency response is very close to the estimated results.

Evaluation

To evaluate the filter response, we can compare the output of the DJ controller to our filter models, through listening test of the filtered music from both systems. (see SampleMusic.m for filtering the sample with modelled filters)

The original audio by Curtis [4]:

Low frequencies filtered on the DJ Controller:

Low frequencies filtered using modelled filter:

Mid frequencies filtered on the DJ Controller:

Mid frequencies filtered using modelled filter:

High frequencies filtered on the DJ Controller:

High frequencies filtered using modelled filter:

As can be heard, the filtered music excerpts from the DJ controller and the modelled filters sound very close, after the volume is normalized.

Conclusion

Through audio experiments and carefully tuning the filter coefficients, I obtained a good model of the filters on the DJ controller. Along with the DJ MIDI sequence parser, now I can accurately resynthesize the music mix with control sequences recorded from a live performance, and I am one step closer to building a DJ system that could mix music like professional DJs do.

References

[1] F. Keiler and U. Zölzer, “Parametric Second- and Fourth-Order Shelving Filters for Audio Applications,” Proc. IEEE 6th Workshop on Multimedia Signal Processing, Siena, Italy, Sept., 2004, p.231.

[2] J. Tackett, Bass / Treble Shelving Filter. https://www.mathworks.com/matlabcentral/fileexchange/16568-bass—treble-shelving-filter?s_tid=prof_contriblnk

[3] J. Tackett, Peaking / Notch IIR Filter. https://www.mathworks.com/matlabcentral/fileexchange/16567-peaking—notch-iir-filter?s_tid=prof_contriblnk

[4] Curtis, No Other Reason, Spinnin Records, 2016. https://soundcloud.com/spinninrecords/curtis-leng-xuan-chen-no-other-reason